|
Home > Chapters > 3 >
All topics
1. Examples of global and local alignments of two proteins
Figures S3.1 and S3.2 present examples of global and local alignments of two proteins.
Figure S3.1. Global alignment of two protein sequences by the Needleman-Wunsch algorithm with enhancements by Smith and Waterman. This example illustrates a global alignment of two hypothetical sequences, sequence 1 = MNALSDRT and sequence 2 = MGSDRTTET. Notice the subsequence SDRT in the two sequences which one might expect to be aligned if the sequences are aligned properly.
|
A. Prepare a 10 x 11 matrix and place sequence 1 across the top of the matrix and sequence 2 down the left side. Leave an extra row and an extra column before each sequence labeled GAP to allow for gaps at the end of alignment. Fill in the extra row and column with the penalties for gaps of length zero to 8. The gap penalty used here is GAP = - 12- 4 (x - 1), where x is the length of the gap. -12 is the penalty for opening the gap in the alignment, and -4 is the penalty for each additional sequence character in the gap. The reason for choosing this particular penalty scheme is discussed below.
B. Fill in the score for each amino acid pair in the matrix. Shown in parentheses are examples for the four possible matches between the first two amino acids. These scores are taken from the log odds form of the Dayhoff scoring matrix at 250 PAMs described in Chapter 3.
C. Calculate the score in each of the above positions. The maximum score of the M/M position is the GAP/GAP score of 0 plus 6 for an M/M match, or 6. The arrow indicates the previous matrix position that was used to obtain a score of 6; i.e., the box labeled with a score of 0. Similarly, the maximum possible score in the N/M position is 6 - 12 (one gap penalty) = -6, that of the M/G position is 6 - 12 = -6, and that of the N/G position is 6 + 0 = 6 (no gap penalty). Note that each sequential row and column must be completed before moving to a lower row or more rightward column.
D. Complete the matrix by choosing at each position the maximum possible score (E). Keep track of all moves made to reach a maximum score at each position in a second matrix, the trace-back matrix (F).
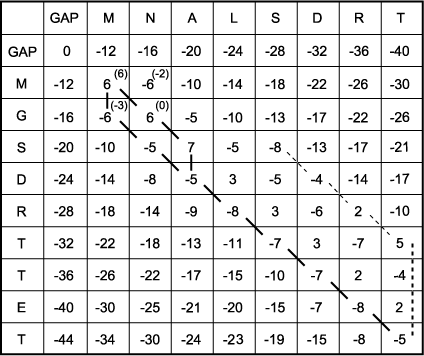 E. The scoring matrix is completed to find the highest score at each matrix position. The process started in C has been continued to fill in the entire matrix with the maximum possible score at each matrix position. The right column and lowest row are then examined for the highest possible score because the alignment is a global one, meaning that the alignment will end only when the end of one of the sequences has been reached. Any remaining unmatched sequence will be opposite gaps. The highest-scoring box in the right-hand column and lowest row is a 5 in row 7. If end gaps were not being penalized, this would be the end of the search for the best score. However, if the alignment were to end here, there are three unmatched positions left in sequence 2, and each will be opposite a gap. Thus, an additional penalty score for three gaps ( -20) corresponding to the heavy dotted line will have to be subtracted from 5, leaving an alignment score of 5 - 20 = -15. By subtracting any remaining end gap penalties from all positions in the last column and bottom row (not shown), one finds that the best score is actually -5 in the right-hand, lowest corner of the matrix obtained by a diagonal move to this position, giving a score of -8+3 = -5.
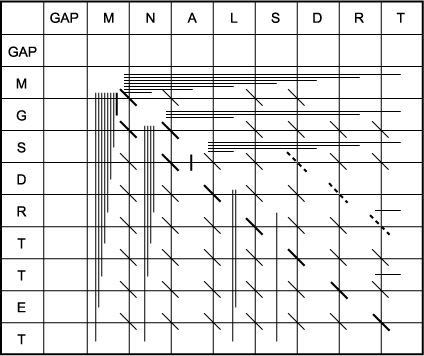 F. The trace-back matrix is used to find which characters align. This matrix shows all of the moves made by the algorithm from one matrix position to another to calculate the maximum score at each position. Because the highest-scoring position in the last row and column is the -5 in the rightmost, lower corner, this position is in the alignment. Thus, the last T in each sequence will be matched. The task is to find a path back through the matrix using the moves made to get to that highest-scoring position and stopping at the beginning of one of the sequences. When the path turns from a previous diagonal move, a gap is placed opposite the next character in sequence 2 if the path turns upward and sequence 1 if it turns to the left. Two paths, shown as darker lines, are possible. These are also shown in part I above and correspond to the alignments 1 and 2 shown below. Note that if end gap penalties were not used, the path shown by the light dotted line in part I would be the correct alignment. This alignment, alignment 3, is also shown below. Note that wherever there are two paths leading to a matrix position, i.e., two possible ways of achieving that score, two alternative alignments will branch from that position. It is not too difficult to see that there are many possible paths through the scoring matrix that represent different alignments.
|
|
sequence 1 M - N A L S D R T
sequence 2 M G S D R T T E T
score 6 -12 1 0 -3 1 0 -1 3 = -5
Alignment 1. Although this alignment has a low and insignificant score of -5, it is the best-scoring alignment that can be made between these two short sequences with the Needleman-Wunsch algorithm with end gaps penalized. Note that the score of -5 is also found at the lowest position in the last column, corresponding to the alignment of the last characters in the sequences. Normally, it only makes sense to use a global alignment method for producing an alignment between sequences that are about the same length and that are expected to align along their entire lengths. The end gap penalty forces the ends to align. For sequences that are quite similar along their lengths, using end gap penalties will not have the dramatic effect that it does in this hypothetical example.
|
sequence 1 M N - A L S D R T
sequence 2 M G S D R T T E T
score 6 -12 1 0 -3 1 0 -1 3 = -5
Alignment 2. This second alignment is found by the trace-back procedure because there were two possible paths at one location in the matrix. This alignment scores slightly lower than the alignment 1 above. The difference is in the placement of a single gap opposite either a G or an S, and in the slightly higher score for the N/S versus the N/G alignment (1 vs. 0). This result illustrates that the dynamic programming alignment method may find more than one alignment having the same or almost the same score. Programs such as GCG GAP and BESTFIT can be set to provide several of these alternative alignments.
|
sequence 1 M N A L S D R T - - -
sequence 2 - - M G S D R T T E T
score 0 0 -1 -4 2 4 6 3 0 0 0 = 10
Alignment 3. (no end gap penalty included). On initial observation, this alignment has a great deal more appeal than the above two and has a much higher score. However, all of the gaps needed to make the alignment have been put on the ends, where they do not count. Leaving out end gaps also makes the analysis less rigorous mathematically (they appear in the rigorous proofs) and leaves doubt as to whether or not evolutionary conclusions may be drawn (Smith and Waterman 1981a,b). There is a positive effect of helping to identify the region of similarity SDRT without scoring end gaps, but using the Needleman-Wunsch algorithm, this region could still be missed if this amino acid pattern was broken by higher-scoring neighboring alignments. The Smith-Waterman local alignment algorithm discussed below is specifically designed to find such conserved patterns of local alignment.
|
Figure S3.2. Local sequence alignment by the Smith-Waterman algorithm.
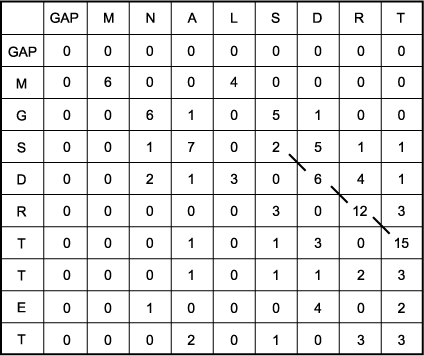 A. Scoring matrix for Smith-Waterman alignment of sequence 1, MNALSDRT, and sequence 2, MGSDRTTET. These same sequences, the PAM250 scoring matrix and gap penalty scores (-12 and -4 for gap opening and gap extension penalties, respectively) for internal and end gaps, were used. The major difference between this scoring matrix and the Needleman-Wunsch matrix is that there are no negative scores in the Smith-Waterman scoring matrix. The effect of this change is that an alignment can begin anywhere without receiving a negative penalty from a previously low- scoring alignment. Once an alignment has been built, it stops when negative alignment scores or the introduction of gaps reduces the following alignment scores to 0. Thus, only a portion of each sequence that was in this high- scoring region will be reported. Note that in this example the initial end gap penalty does not have any effect because all first row and column scores are 0, the minimum allowed by the Smith-Waterman algorithm. Because a gap penalty at the end of the alignment produces a score of zero, the end gap penalty similarly has no effect.
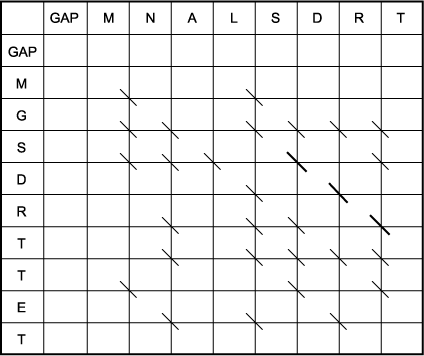 B. The trace-back matrix of the above Smith-Waterman scoring matrix. To find the optimal local alignment, the highest-scoring position in the scoring matrix is located (15), and the trace-back from this position is followed up to a zero in the matrix. The resulting sequence alignment is shown below. As opposed to the complex moves in the Needleman-Wunsch matrix, which are designed to test many combinations of matches, mismatches, and gaps, only simple diagonal moves were made in the Smith-Waterman matrix. Thus, there is only one alignment starting from the highest position. However, many other lower-scoring alignments are apparent, such as the second highest-scoring alignment of MNA with MGS starting at the position that scores 7. Note that this second alignment does not include any of the same amino acids, and not even any of the same aligned amino acids, that were used in the first alignment. It is possible to have multiple local alignments that do use the same aligned amino acid pairs, as there was in the global alignment example given above, but there are no examples in this matrix. The distinctions regarding which alignments use the same aligned pairs, which use the same residues in a different alignment, and which use entirely different residues are described in Chapter 3.
sequence 1 S D R T
sequence 2 S D R T
score 2 4 6 3 = 15
|
C. Sequence alignment determined by the above procedure. Note that the score of the alignment is the same as that shown by the highest-scoring position in the scoring matrix. The inclusion of any additional sequence would reduce the score below 15.
|
|
2. Equivalency of similarity and distance algorithms
Smith and Waterman (1981a,b) showed that the Needleman-Wunsch algorithm based on maximizing similarity scores and the Sellers algorithm based on minimizing distance scores were equivalent, if the following is true:
| sim (ai, bj ) + dist (ai, bj) = sMAX |
(S1) |
| dk = sMAX x k /2 + wk |
(S2) |
where sim (ai, bj) and dist (ai, bj) are the respective distance and similarity scores between characters dist a in one sequence and dist bj in the second; sMAX is the maximum possible similarity score for any pair of different characters; dk and wk are the respective gap scores used in the distance and similarity methods for a gap of length k. In written form, (S1) the sum of the distance and similarity scores for two different characters should be equal to the maximum similarity score used and (S2) the weight assigned to gaps in the distance score should be larger than the Needleman-Wunsch alignment gap score by one-half the length of the gap times the largest similarity score used. For two sequences a = a1a2... an and b = b1 b2...bn of lengths m and n, respectively, the resulting relationship is also true,
| S(a, b) + D (a,b) = sMAX(n + m) / 2 |
(S3) |
where S(a, b) and D(a,b) are the maximum similarity and minimum similarity scores obtained by the respective Needleman-Wunsch and Smith-Waterman dynamic programming algorithms, respectively.
When simple scoring systems are used, these equations provide a way to convert similarity to distance scores, and vice versa, for individual sequence characters and alignment scores. The conversions are more complicated for more sophisticated scoring schemes, such as a PAM scoring matrix for scoring amino acid similarities. For now, it is important to realize that similarity and distance methods produce approximately the same alignments, provided that the equivalent scoring schemes are used. If one is to draw the correct evolutionary inferences, however, similarity scores should be converted to the equivalent distance scores.
3. Improvements in time and memory efficiency for global alignments
The original Needleman-Wunsch dynamic programming algorithm allowed single gaps and took N x M steps to align two sequences of length N and M. Subsequently, Waterman et al. (1976) and Smith and Waterman (1981a,b) extended this algorithm to allow for multiple-sized gaps in the alignment, and the alignment then took N x M2 steps (where N is the shorter sequence). Similarly, the alignment algorithm developed by Smith and Waterman also required N x M2 steps. The dynamic programming algorithm was improved in performance by Gotoh (1982) by using the linear relationship for a gap weight wx = g + rx, where the weight for a gap of length x is the sum of a gap opening penalty (g) and a gap extension penalty (r) times the gap length (x), and by simplifying the dynamic programming algorithm. He reasoned that two of the terms that are maximized in the dynamic programming algorithm and designated here Pij and Qij depend only on the values in the current and previous row and column, as indicated below.
Improved dynamic programming algorithm of Gotoh (1982)
The similarity score is written as
Si,j = max { Si-1,j-1 + si,j, Pi,j, Qi,j }, where
Pi,j = max { Si-x,j -wx }, and Qi,j = max { Si,j-x - wx }
1<x<i 1<x<j
P may be obtained in a single step since,
Pi,j = max { Si-1,j - w1, max ( Si-x,j - wx }
2<x<i
= max { Si-1,j - w1, max ( Si-1-x,j - wx+1 }
1<x<i-1
= max { Si-1,j - w1, max ( Si-1-x,j - wx - r }
1<x<i-1
= max { Si-1,j - w1, Pi-1,j - r }
where the penalty of a gap of length x is given by,
wx = g + rx
and g is the gap opening penalty and r the gap extension
penalty.
Similarly,
Qi,j = max { Si,j-1 - w1, Pi,j-1 - r }
Although this procedure can align sequences of lengths N and M (N < M) in M x N steps, these operations still require the storage of three matrices in memory of size M x N. Myers and Miller (1988) were able to reduce this memory requirement by storing enough information to compute the similarity score in N units of memory. This saving of memory space was achieved by recognizing that calculation of each matrix row by the Gotoh method depends only on the values of the current and most previously calculated rows. Thus, only matrix values in those rows plus a few other numbers need to be saved in an array, and old values can be overwritten by new ones as new rows are calculated. Because local and global alignments are computed the same way, these same improvements can be used for producing both types of alignments.
Furthermore, Myers and Miller were able to save additional memory space required for storing the trace-back matrix that keeps track of the moves giving the best score at each matrix position. In doing so, they also reduced the number of sequence comparisons that must be made to find an optimal alignment. The trace-back matrix requires M x N memory positions. Myers and Miller utilized the fact that the same best alignment is obtained by the dynamic programming algorithm starting at the sequence beginnings and moving forward down the sequences as starting at the sequence ends and moving backward along the sequences. In their method, a subalignment is started in the forward direction, but does not go beyond the half-way point along the first sequence. Another alignment is started from the far end of the sequences, ending at the same half-way point in the first sequence. At some position J in the second sequence, these forward and backward alignments must converge on an optimal midpoint in the alignment, as illustrated in Figure S3.3. The sum of the scores is the optimal score of aligning the full sequences, after correcting for subalignments that both end in deletes. In breaking down the trace-back analysis this way, called the divide-and-conquer approach by Hirschberg (1975), two improvements are realized: (1) only one-half as many sequence positions have to be compared by the dynamic programming algorithm to find the optimal alignment (the area inside the colored rectangles), and (2) only one-half as much memory is needed to keep track of the moves. One other round of divide-and-conquer would require filling in only the brown area of the matrix, thus halving the requirement again. In this manner, dividing up of alignments into subalignments can be repeated several times to reduce the memory requirement even further to approximately a linear function of sequence length (Fig. S3.3). By confining sequence comparisons to a narrow band of interest in the dynamic programming alignment grid in combination with the above divide-and-conquer method, such as in aglobal alignment of related sequences of approximately the same length, the algorithm can be made even more efficient (Chao et al. 1994).
A similar strategy may be used to obtain a local alignment as a linear function of sequence length. The end points of the local alignment are first found by using the Smith-Waterman algorithm and the Gotoh method to reduce the computational time. The trace-back path is then found by applying the divide-and-conquer approach within the corresponding area of the matrix defined by these end points (Chao et al. 1994). As a result of these changes, the dynamic programming algorithm can be more easily run on smaller computers without compromising the ability of the method to find an optimal alignment. Most dynamic programming programs for sequence alignment use these more efficient methods. Many of the above formulations that reduce time and space for calculating optimal sequence alignments have depended on a re-formulation of the dynamic programming algorithm using mathematical graph theory by G. Myers, W. Miller, and their colleagues. Although a description of the graph theory method is beyond the scope of this chapter, the formulation is not too different from that given above. However, the method provides a level of mathematical rigor and insights and a more critical view of details of the sequence alignment problem. Readers interested in the application of graph theory to the problem of sequence alignment should consult the review by Chao et al. (1994).
|
Figure S3.3. The divide-and-conquer approach of Myers and Miller (1988). Whereas the full dynamic programming method requires the entire matrix of size M x N to be filled, where M and N are the sequence lengths, the new approach only requires the positions that are shaded in the graph.
|
|
Finding near-optimal alignments
The dynamic programming alignment program reports only the highest-scoring or optimal sequence alignment. As discussed previously, there may be other important alignments with scores as high as the optimal one. These may be alternate paths back through the dynamic programming matrix starting at the same high-scoring position. These alignments will use some of the same aligned residues that were also used in the optimal alignment. Other alignments may use the same residues but have them aligned differently. Yet a third kind of alternative alignment may use entirely different amino acids to achieve a range of possible alignments.
The LFASTA program uses the FASTA algorithm to report a series of alternative alignments of proteins, and PLFASTA plots the alternative alignments in a form much like a dot matrix plot (Pearson and Lipman 1988; Pearson 1990). Another method of finding near-optimal alignments is to design a method for identifying the highest-scoring alignment, then the next highest-scoring, and so on, in that order. To accomplish this, Saqi and Sternberg (1991) change the values in the scoring matrix after the first alignment has been found to be biased against that alignment and to favor others the next time.
Waterman and Eggert (1987) devised another method for finding a series of local alignments that is widely used. After finding the highest-scoring alignment beginning at position i in sequence 1 and position j in sequence 2, the matrix position Hi,j that initiates this alignment is given a score of zero. The H matrix values (and also the Gotoh P and Q matrix values), which are below and to the right of this position, are then rescored for as far in the matrix as the recalculation continues to change the values. This recalculation has the effect of removing the highest-scoring alignment and any other alignment that uses the same residue pairs as the first alignment, but the same residues may be used in a different alignment. The rescored matrix is then scanned for the next highest local similarity score and the path leading to it provides the next highest-scoring alignment. The Waterman and Eggert method calculates these alternative alignments in far less time than taken to produce the original scoring matrix. A more space-efficient version of this method using graph theory has been described (Huang and Miller 1991; Chao et al. 1994).
Another method of identifying near-optimal alignments is to score all alignments that achieve a similarity score greater than a specified minimum (Chao et al. 1994). In the above section, an optimal midpoint in an alignment was found by forward-backward passages of the dynamic programming algorithm, as illustrated in Figure S3.3. A similar procedure is used here on a rectangular portion of the original dynamic programming matrix, with two changes, as illustrated in Figure S3.4: (1) the range of midpoints that give a score of at least the set minimum is located, and (2) the procedure is repeated with midpoints along the second sequence. The result is a set of scores along both midpoints of the matrix that define a band of possible alignments, illustrated by the area between the dark lines. The alignment paths follow a set of adjacent squares as in Figure S3.3, except that the sizes of the squares are adjusted and the squares overlap enough horizontally so that the boundary lines can pass from one square to the next. The result is a band of space that fills enough of the scoring matrix so that all possible alignment paths can be found.
|
Figure S3.4. The divide-and-conquer method used to locate points on all alignments that exceed a minimum score. Shown is a portion of the dynamic programming alignment matrix between positions i1 and i2 in sequence 1 and j1 and j2 in sequence 2. All alignments that achieve the minimum score lie within the colored area and between the dark lines.
|
|
4. Discussion of choice of gap penalties
Some additional gap penalties that are in use in addition to those listed in Table 3.10 in the book are given in Table S3.1. Note that these do not necessarily provide a local alignment that can be tested statistically but may have instead been found useful for some specific purpose, such as a global alignment of similar proteins of the same length.
Table S3.1. Examples of gap opening and extension penalties used by sequence alignment programs. These values are examples that should produce a reasonable alignment in most cases. Other values should also be tried.
| A. DNA ALIGNMENT PROGRAMS |
|
Program1
|
Type of alignment
|
Match score
|
Mismatch score
|
Gap opening penalty2
|
Gap extension penalty2
|
| GCG Gap |
global
|
10
|
0
|
-50
|
-3
|
| ALIGN |
global
|
5
|
-4
|
-16
|
-4
|
| GCG Bestfit |
local
|
10
|
-9
|
-50
|
-3
|
| LALIGN |
local
|
5
|
-4
|
-16
|
-4
|
| LFASTA |
local
|
5
|
-4
|
-16
|
-4
|
|
| B. PROTEIN ALIGNMENT PROGRAMS |
|
Program1
|
Type of alignment
|
Match and mismatch scores
|
Gap opening penalty2
|
Gap extension penalty2
|
| GCG Gap |
global
|
BLOSUM62 values
|
-143
|
-4
|
| GCG Gap |
global
|
BLOSUM50 values
|
-123
|
-2
|
| GCG Gap |
global
|
PAM250 values
|
-12
|
-4
|
| GCG Gap |
global
|
PAM120 values
|
-11
|
-8
|
| ALIGN |
global
|
BLOSUM50 values
|
-16
|
-4
|
| ALIGN |
global
|
PAM250 values
|
-14
|
-4
|
| GCG Bestfit |
local
|
BLOSUM62 values
|
-143
|
-4
|
| GCG Bestfit |
local
|
BLOSUM50 values
|
-123
|
-2
|
| GCG Bestfit |
local
|
PAM250 values
|
-12
|
-4
|
| GCG Bestfit |
local
|
PAM120 values
|
-11
|
-8
|
| LALIGN |
local
|
BLOSUM50 values
|
-16
|
-4
|
| LFASTA |
local
|
BLOSUM50 values
|
-16
|
-4
|
| SSEARCH4 |
local
|
BLOSUM50 values
|
-12
|
-2
|
| SSEARCH4 |
local
|
J093 values
|
-10
-16
|
-4
-2
|
| SSEARCH4 |
local
|
JTT160/JTT200 values
|
-14
|
-2
|
| SSEARCH4 |
local
|
BLOSUM62 values
|
-6
-8
|
-4
-2
|
| SSEARCH4 |
local
|
PAM250 values
|
-10
-12
-14
|
-2
-2
-2
|
| SSEARCH5 |
local
|
BLOSUM45 values
|
-10
-12
-12
|
-10
-12
-12
|
| SSEARCH5 |
local
|
Gonnet92 values
|
-10
-12
-12
|
-10
-12
-12
|
|
1 The programs listed here include the Genetics Computer Group sequence alignment programs GAP and BESTFIT and examples of the alignment programs distributed by W. Pearson as a part of the FASTA package. LFASTA was in the original FASTA programs (Pearson and Lipman 1988), ALIGN is derived from the Meyers and Miller (1988) algorithm, and LALIGN and SSEARCH are derived from the Huang and Miller (1991) algorithms. These programs run efficiently on a PC or Macintosh and may be obtained by anonymous FTP from ftp.virginia.edu/pub/fasta.
2 The GCG programs up to vers. 9.1 are designed to use the gap opening penalty plus a single gap extension penalty for a gap size of 1 and then to add a gap extension penalty for additional gaps. The FASTA programs use a different method: Only the gap opening penalty is used for a gap size of 1, and the extension is not used until the gap is longer. When gap penalties are recommended by investigators, it is important to note whether the gap opening penalty already includes an extension penalty if the penalties are to be used correctly with the programs. Many scoring matrices, such as the BLOSUM matrices, will include recommended gap penalties in the file. Due to an oversight of this type, the gap opening penalties for some of the GCG programs shown above (3) should be reduced by a single gap extension penalty. The GCG programs base gap penalties on matching the range of values in the scoring matrix. For the remaining programs, the optimal penalties have been chosen by W. Pearson and based on experimentation and statistical analysis (Pearson 1995).
3 Use a value of -10 instead of these default values in the GCG versions 9.1 and earlier.
4 SSEARCH is a local alignment program that is designed for searching through protein sequence databases to locate homologous sequences. The values shown are based on a statistical study by Pearson (1995), which was designed to find the most members of the same protein superfamily. The matrices shown are the best performers when combined with the gap penalty combinations in the last two columns. Any local alignment program for sequence analysis should provide identical results. The BLOSUM62 matrix shown is that used by BLASTp, and is given in 1/2-bit units.
5 For these scoring matrices to perform as well as the ones listed above, the similarity scores were scaled. More recent scoring procedures are discussed in Pearson (1996, 1998).
|
An appropriate set of gap penalties must be made corresponding to each
type of scoring system used for matches and mismatches to place gaps where
they will increase the overall score of the alignment. There are no hard
and fast rules for choosing gap penalties, but there have been several
studies that provide guidance. Fitch and Smith (1983) analyzed the
influence of gap penalties on the alignment between two rows of codons in
the chicken α- and β-hemoglobin sequences, chosen because the
amino acid sequence reveals two gaps in this region. The ends of these
sequences should align, but the codon alignment should reveal two gaps
corresponding to extra codons in the β-hemoglobin gene. The
Needleman-Wunsch alignment method was used, with and without weighting end
gaps, and varying both the gap opening and gap extension penalties
(g and r in wx = g + rx). First,
perhaps not surprisingly, regardless of g and n, the presumed
correct solution was not found unless end gaps were weighted. Second, if
end gaps were weighted, varying g and r provided a large
number of possible alignments, including the correct one.
Using this example of a nucleic acid sequence alignment as a guide, the
authors make the following general recommendations concerning choice of gap
penalties and related issues:
- Both the gap and its length should be weighted.
- Both g and r should be non-zero.
- The value of g + r should be greater than the maximum score used for a match if insertions and deletions are considered to be rarer than nucleotide substitutions.
- The value of g strongly influences the number of gaps introduced into a region separating two closely matching regions.
- If the ends of the two sequences are not known to be equivalent, e.g., as in two sequence fragments of unequal length but with random start and end points, end gaps should not be weighted. Conversely, if the ends are equivalent, as in two sequences of the same length and starting and ending at common locations such as in particular codons, end gaps should be weighted.
- The Needleman-Wunsch similarity method offers the advantage of scoring or not scoring end gaps that is not available in the Seller's distance method.
- Match (or mismatch) values other than 0 or 1 should be allowed, such as for transitions/transversions in DNA sequences and amino acid differences in protein sequences.
- A good sequence alignment program should provide an option for determining the probability that the optimal alignment obtained could have been obtained by a chance alignment of nonhomologous sequences.
In aligning 1.7 x 106 related proteins to formulate the Gonnet92 amino acid scoring matrix (described above), Gonnet et al. (1992) and Benner et al. (1993) found that the probability of a gap of length k decreases as a function of increasing gap length over the range of observed gap lengths (1 to 60 amino acids), and that the length distribution is independent of the degree of similarity (or evolutionary distance) between the proteins. Thus, short gaps of a few positions are more common than large, both between closely and more distantly related proteins. The authors recommended the following nonlinear equation (S4) for use with the standard log odds Dayhoff matrix at a given PAM distance.
| 10 log10(P) = -36.31 + 7.44 log10 |
|
| (PAM distance) - 14.93 log10 (k) |
(S4) |
where 10 log10 (P) is the probability of a gap of length k expressed in the units of the log odds form of the PAM250 matrix [units of 10 x log10 (observed frequency of substitution of amino acid 1 by amino acid 2) / expected frequency of substitution]. This equation gives gap penalties for the PAM250 table for gap lengths of 1-5, respectively, of -18.5, -22.9, -25.6, -27.5, and -29.0. These authors also fit their data to a linear equation for ease of computation, and state that the above penalties for the 250 PAM matrix are approximately the same as a linear function of the form 10 log10 (P) = -19.06 -1.65 k, corresponding to a gap opening penalty of approximately -19 and a gap extension penalty of -1.65 per gap unit. These penalties are quite a bit larger than the optimum values used in most situations. However, the authors propose that these penalties provide another way to examine protein sequences for a distant relationship.
One analysis was performed on scores from alignments of random protein sequences. Protein sequence alignments use a scoring matrix with both positive and negative values, and sometimes with all positive values. For local alignments, the average score of a matrix should be negative, because otherwise the score of any alignment would continue to grow with length. For example, using current estimates of an average amino acid composition of proteins, the average score of the Dayhoff log odds matrix at 250 PAMs is expected to be -0.81, which favors finding an optimal alignment. If a constant of 0.9475 is added to the values of the PAM250 log odds matrix to produce a slightly positive average value, a higher alignment score for both global and local alignments is obtained. If the gap opening andextension penalties are decreased under these conditions, the score of the global alignment increases and that of the local alignment increases linearly, not logarithmically. What this linear relationship means is that there is a far better resolution of the various alignments that arise as the gap penalties are varied. Using alignment of the light and heavy chains of the immunoglobulin variable domain as an example, Vingron and Waterman (1994) were able to resolve all of the four known optimal local alignments by using a positive scoring version of the PAM250 matrix and varying the gap opening and extension penalties. Both gap penalties appeared to play a decisive role in obtaining the best alignment. For the molecular biologist who wishes to explore a range of possible local alignments of protein sequences by varying gap penalties, use of a PAM250 or BLOSUM scoring matrix modified to a small positive average value would appear to provide an improved resolution of the possible alignments. It is also important to keep the average value of the matrix as small as possible, because in aligning a short sequence with a long one, use of a high average matrix value will lead to an alignment with fewer deletions in the shorter sequence than in the longer one (Dayhoff et al. 1983).
In another study, Pascarella and Argos (1992) examined the size and distribution of gaps in known protein structures and found that their distribution does not follow that predicted by wx = g + nx formulation. Choosing only proteins whose three-dimensional structures are known, they carefully aligned the proteins in 32 structural families using structural criteria and examined where the gaps were located with respect to the known structural features. These proteins varied in the degree of residue identity from <10% to >60%, but most were 10-20% identical; i.e., in most of the aligned sequences the percentage of amino acids in the same column that was identical was 10-20%. Thus, the study compared proteins that had undergone a significant degree of evolutionary change. A filtering procedure was also used to avoid overrepresentation of features that were repeated in larger groups of homologous proteins. Despite the varying evolutionary distances among these proteins, the most common length of a gap (a gap was called an indel for an insertion/deletion event) regardless of distance between the sequences was 1. In this respect, the results agree with those of Gonnet et al. (1992), described above. Above a residue identity level of 25% in the alignment, the average gap length was 2-3, and below 20% it was 4-5. The few gaps larger than 5 that were observed were also found at all levels of identity. Thus, during evolution of protein structure, an equilibrium appears to be reached in the insertion and deletion of extra amino acids in the gap regions.
The location and distribution of gaps was also analyzed by Pascarella and Argos (1992). The average distance between gaps decreases as the percent identity decreases, eventually reaching a value of <10, which is close to the average length of α-helices and β-strands. In fact, most of the indels were found to occur in regions that are between secondary structural elements (loops, coils, and turns) and to involve amino acids that tend to be found in such intervening regions; i.e., polar and/or small amino acids including Gly, Pro, Asn, Ser, Asp, and Thr. In the few cases where insertions in secondary structural elements were found, these were usually short extensions to the termini of such structures. In conclusion, alignments of structurally related proteins have revealed that gaps greater than 5 seldom occur even in distantly related proteins. Thus, the gap weighting function should increase greatly once a gap of 5 has been reached, or else the sequence alignment program should not allow gaps longer than 5 to occur. When using the GCG dynamic programming alignment programs, the maximum gap length may be set with the parameter PENALIZEDLENGTH.
Vogt et al. (1995) have suggested gap opening and extensi on penalties for use with modified amino acid scoring matrices to find the optimal alignments between proteins assuming that they share a structural relationship. Altschul and Gish (1996) and Pearson (1996; 1998) have found that use of appropriate gap penalties will provide an improved local alignment based on a statistical analysis. These studies are further described in the book.
5. Updates to PAM amino acid scoring matrices
The Dayhoff data set has been augmented to include the 1991 protein database (Gonnet et al. 1992; Jones et al. 1992). The ability of the Dayhoff matrices to identify homologous sequences has also been extensively compared to that of other scoring matrices.
The Gonnet et al. (1992) revised PAM matrix, also known as the Gonnet92 matrix, was prepared by first ordering the sequences by organizing them through a type of index. By this ordering method, the sequences are effectively organized into a tree in which similar sequences should be represented by nearby branches on the tree. Thus, the ordering provides a way to quickly locate similar sequences for alignment. Because aligning the sequences was a much more time-consuming process, this clustering greatly reduced the computational time needed. Alignments between closely related and more distantly related sequences were produced by the Needleman-Wunsch dynamic programming method using the original Dayhoff PAM matrices as a starting point. From these alignments, new scoring matrices were calculated for protein pairs separated by the same distance, and then these matrices were used to refine the alignments, which, in turn, were used to produce a final matrix. Changes in amino acids between all pairs of aligned sequences at the same level of similarity were then calculated. These distributions were then adjusted to the same level of similarity by a matrix multiplication method similar to that used by Dayhoff. Finally, these matrices were used to calculate a new average scoring matrix of distance 250 PAMs, referred to as the Gonnet92 scoring matrix. Benner et al. (1994) later published a set of substitution matrices at 250 PAMs based on the same data, except that the data for sets of aligned proteins at the same PAM distance levels (decreased similarity) were combined and used to produce a set of scoring matrices at 250 PAMs identified as BennerN matrices, where N is the approximate PAM distance between the sequences aligned to score the amino acid substitutions. Recommended gap penalties were published along with these matrices (Benner et al. 1993).
At least two significant changes between this method and that used by Dayhoff are apparent: (1) the absence of tree-building to infer the amino acid changes occurring in each set of homologous proteins, which would in any case have been a very difficult task for this many proteins, and (2) proteins separated by PAM distances between 6.4 (6% difference) and 100 (>50% difference) were used to score amino acid changes that were used to produce the new matrix, as opposed to the PAM15 distance (approximately 15% difference) used by Dayhoff. It is much more difficult to align more distant proteins, and the placement of mismatches and gaps in the alignment will determine which substitutions will be scored. An improvement would be to use multiple sequence alignments to locate the gaps. The problem is worsened by using an already existing scoring matrix to make the alignment because the first matrix will then influence the scoring of the second. This problem is much reduced when substitutions in closely related sequences are scored, because a realistic alignment can be readily produced. If one accepts the Dayhoff Markovian model of protein evolution as a set of random amino acid changes, then for high PAM distances, the probability that a significant fraction of the observed amino acid changes represents two or more sequential changes greatly increases. In addition, some previously changed amino acids are more likely to have reverted to the original one. For sequences that differ by an average number of x residues, the distribution of the actual number of mutations should be approximately given by the Poisson distribution Pn = e-x xn / n!, where Pn is the probability of n differences. For sequences that are 15% different, as used by Dayhoff, P0 = 0.86, P1 = 0.13, and P2 = 0.01. Thus, only 8% of the amino acid changes sampled are expected to be double changes. But for sequences that are 30% different, this ratio is 14%, and for sequences that are 40% different, 20%. Thus, scoring more distantly related sequences, as performed by Gonnet et al. (1992), does not permit one to evaluate as well the single amino acid changes that occur during a Markovian evolution process because many of the resulting amino acids have been changed a second time. Due to such concerns, it would appear that the Gonnet92 matrix is not a reasonable substitute for the Dayhoff PAM250 matrix as a way to score evolutionary changes in proteins. Rather, it is a hybrid matrix between the Dayhoff PAM model and the BLOSUM model described in Chapter 3.
Another substitute for the Dayhoff PAM250 matrix is an amino acid substitution matrix named PET91 (pair exchange table for year 1991), and also called JTT250 (Jones et al. 1992). This matrix was also based on the comparison of a large number of protein sequences by clustering the sequences on a tree as a rapid method for identifying similar sequences. This method was slightly different from that used by Gonnet et al. (1992) and was based on identifying similar sequences through their having the same complement of amino acid triplets. The resulting matrix was also a log odds matrix at 250 PAMs, although JTT matrices at other evolutionary distances may also be calculated by the program CALCPAM, which may be obtained from the authors. The new data set included 59,190 accepted point mutations in 16,130 protein sequences, a much smaller number than that compared by Gonnet et al. (1992). The JTT matrix was based on sequences that were >85% similar, and in this respect was identical to the original Dayhoff analysis, whereas Gonnet et al. (1992) also used alignments from more distantly related sequences. Jones et al. showed that their sequence clustering method predicted the same or similar frequencies of amino acid changes in the original Dayhoff data set, although the method of inferring evolutionary change was quite different. These new mutation data matrices (MDM), Gonnet92 and JTT250, are compared to the original Dayhoff MDM matrix at 250 PAMs in Table 3.3 in the book. The units in this log odds table are log10 x 10, as is the original MDM of Dayhoff at 250 PAMs.
There are significant differences both between the new Gonnet92 and JTT250 matrices and the old Dayhoff matrix at 250 PAMS (row 1) and also between the Gonnet92 (row 2) and JTT250 (row 3) matrices. The most striking differences are in the substitutions between C (Cys) and W (Trp) and many of the other amino acids, of which many more had been observed than in the original Dayhoff data set, and some were not oberved at all previously. For example, the log odds score between W (Trp) and C (Cys) increased from -8 to -1 and +1, an increase of 5- to 8-fold in probability. In the new protein comparisons, C (Cys) and W (Trp) were exchanged, whereas they were not exchanged in the original Dayhoff analysis. Other amino acid exchanges were rare in the new tables, as in the original data. For example, W (Trp) and N (Asn) were only seen to exchange twice in the JTT data set. A similar but less pronounced increase in score occurred with W (Trp)/G (Gly) and M (Met)/C (Cys). These differences seen in the newly derived matrices are also reflected in a decreased score for aligning these same amino acids (C and W) with each other in sequences.
There are also some large differences between the Gonnet92 and JTT250 matrices, both of which were supposed to substitute for the original Dayhoff PAM matrices. These differences may be attributed to the overall number of sequences compared and their relatedness. For example, the Gonnet92 log odds score for W (Trp)/ Y (Tyr) is 4,whereas that of JTT250 is 0, a difference in probability of 2.5-fold. There are also a number of examples of variations in log odds scores of 2 (1.6-fold probability) and 3 (2-fold probability). On the basis of the differences in the scoring matrices, the best recommendation that can be made is to use the JTT matrices as a more modern substitute for the Dayhoff matrices. The Gonnet and Benner matrices are useful for scoring amino acid changes between proteins that are more distantly related, because no underlying evolutionary model was used to prepare these matrices. A comparison of these matrices for aligning sequences is given below.
6. Comparisons and uses of amino acid scoring matrices
As outlined in the text, the theoretical basis for performing a sequence alignment is to determine whether or not the sequences are homologous, i.e., derived from a common ancestor sequence. The degree of similarity found can indicate how much separation has occurred, expressed in PAM distances. Because different matrices are designed for answering different questions about sequence similarity, it is very difficult to know how to compare them appropriately, and also how to use them to analyze evolutionary relationships. Second, the ability of these matrices to produce alignments needs to be assessed by using known alignments assessed by an independent criterion. The same tests are not appropriate for all matrices because they are based on different criteria. Third, the sequence alignments used for testing matrices should be a representative collection of all known sequence classes and should not contain an overrepresentation of similar sequences, nor should they be the same sequence alignments that were used to produce the matrix. Fourth, each scoring matrix has a particular range of values, some log odds values of positive and negative values, and others a simple scale of values that are all positive. To use these matrices, a different gap penalty score that produces reasonable alignments must be used for each. These penalties are usually not published or well known, thus throwing a level of uncertainty into the alignments obtained, and also into the reliability of the matrix comparison analyses. When investigators publish a new scoring matrix, they usually devise a scheme for comparing the ability of that particular matrix to others for producing reliable alignments. These types of analyses often overlook the purposes of different matrices and fail to recognize differences in the underlying models of protein evolution implied in their construction. With this sobering introduction in mind, some matrix comparison studies are discussed below.
Comparison of amino acid scoring matrices poses several problems for the reader to sort out. First, many extremely useful scoring matrices are not based on an explicit model of protein evolution, as are the Dayhoff matrices. Instead, they are designed to locate sequence similarity as a basis for some other common feature between proteins, such as structure, biochemical function, or a family relationship, because they were generated by examining similarity in sequences that share such features in common. These matrices include the BLOSUM, Gonnet92, and JO93 matrices. Recent research (Henikoff and Henikoff 1993; Pearson 1995; 1996; 1998) has shown that, for the majority of sequence analysis projects, these matrices are the most likely to identify a relationship or to find related sequences in a database search, provided that appropriate gap penalties are chosen. At the same time, these matrices are not as useful for discovering evolutionary relationships, because an explicit model of protein evolution was not used in their generation (Altschul et al. 1994). If evolutionary relationships are to be emphasized, the PAM and JTT scoring matrices offer the best analysis, provided that the matrix that corresponds to the evolutionary distance between the sequences and appropriate gap penalties for that matrix are used.
Amino acid scoring matrices are used for two types of analyses. One is to produce alignments and score similarity between two or more protein sequences for reasons identified above, not forgetting that the goal is to identify homology. A second purpose is to find sequences similar to a test sequence in a database search such as by the BLAST or FASTA programs. This second function of the scoring matrices is quite different and is discussed in Chapter 7. For producing sequence alignments, there is no best scoring matrix for every purpose, and the best choice for the investigator is to try several. For the Dayhoff matrices that are based on a particular model of protein evolution, the best alignment is theoretically expected when the correct matrix is used. This matrix should be based on the same evolutionary distance as is apparent between the sequences. The Dayhoff matrix at 250 PAMs of evolutionary distance corresponds to proteins that should be about 20% similar. This level of similarity is within the "twilight zone" of alignment in which most alignments are difficult to prove or to believe. Perhaps in this case, using a Smith-Waterman program will reveal a local area of similarity that is more convincing than a Needleman-Wunsch program. Sequences that are 60% similar are separated by approximately 60 PAMs, 50% similar by 80 PAMs, 40% similar by 120 PAMs, and 30% similar by 160 PAMs of distance. These matrices are widely available and more can be generated by the PAM program (distributed with the BLAST package of programs) to accommodate any distance. As a more appropriate matrix is used, the alignment should improve and be reflected in an increase in the score of the alignment, provided that other factors such as the gap penalty are also adjusted in a reasonable way.
In an early study of matrix comparisons, the ability of several of these matrices to identify distantly related sequences has been compared with the Dayhoff PAM250 matrix (Feng et al. 1985, Doolittle 1989). The PAM250 matrix proved to be the best, but was closely followed by the structural and genetic code matrices. For comparing similar sequences, the genetic code, amino acid side chain, and PAM250 scales were equally useful.
Abagyan and Batalov (1997) performed a study of the value of scoring matrices in predicting global alignments between structurally related protein sequences. They examined alignment scores among a large number of proteins whose structures were either known or presumed to be known based on structural alignments. The objective was to find whether or not the alignment score of other similar features, such as percent identity or similarity, was a reliable indicator of a structural relationship. If so, scores between structurally related proteins should be high and those between unrelated proteins should be low. The proteins analyzed had been collected in a database known as the HSSP (homology-derived secondary structure of proteins) database (Sander and Schneider 1991) (see Chapter 9 in the book). They represented members of the same structural family and also of different structural families. These families had been identified in the SCOP (structural classification of proteins) database (Murzin et al. 1995). The various sequence combinations were aligned by the global Needleman-Wunsch alignment algorithm without end gap penalties, the latter being chosen to favor the location of similar domains in different positions in the sequences being compared. The scoring matrices were similar to those used above by Vogt et al. (1995), including the positive scoring matrices. To standardize the comparisons between matrices, they were each normalized such that the sum of the diagonal scores when adjusted for residue frequency added up to 1. A number of different gap opening and extension penalties were also tried. Because these values were chosen to be optimal for the normalized matrix, they will not work for others using the standard scoring matrices. This paper also has an excellent discussion of the statistical significance of alignment scores. The results of this analysis showed some similarities but also some differences with those of Vogt et al.
A similar finding was that the Gonnet92 and BLOSUM50 scoring matrices, normalized as described below, performed the best. Other BLOSUM matrices performed almost as well. These normalized penalties (adjusted by us to the regular scores for these matrices in parentheses) were 2.4 (11) and 0.15 (1) for the Gonnet92 matrix and 2.0 (13) and 0.15 (1) for the BLOSUM50 matrix, for the gap opening and extension penalties, respectively. The surprise was that the all-positive matrices that had performed the best in the Vogt et al. (1995) study performed the worst in this one. It is not clear why this should be so. One possibility is that a different criterion for success was used. The criterion here was fold recognition, whereas the former study was based on a full sequence alignment score between the sequences of structurally related proteins. The authors conclude that several different scoring matrices should be used because one alone, such as the Gonnet92 matrix, produces an alignment score that suggests a relationship between unrelated proteins; i.e., it is not very selective and sometimes fails to demonstrate a relationship when there is known to be one.
Another method of testing a scoring matrix and gap penalty combination is to perform a search of a sequence database with a known member of a protein family and to find how many members of the family are found when the same matrix/penalty is used. In analyses of this kind in which gap penalty was not considered, the BLOSUM62 matrix outperformed the PAM250 matrix in finding more members of 504 different families on the Prosite database (Henikoff and Henikoff 1993). Subsequently, Henikoff and Henikoff (1993) showed, using representatives of the 560 families that were used to produce the BLOSUM matrices, that the BLOSUM62 matrices also performed better in this same test than a series of Dayhoff (80-250) and JTT (80-220) PAM matrices and the matrix, and slightly better than other BLOSUM matrices (45, 50 , 80, and 100) and a structure-based scoring matrix (STR, similar to JO93).
Brenner et al. (1998) have conducted a third such detailed study of the ability of sequence alignment programs to recognize proteins that are related by structure and not by sequence. They argue that basing the evaluation of a system on the recognition of proteins in families previously defined by sequence similarity begs the question of finding true homology, which should be based on structure. Therefore, they developed two new databases of protein structural domains derived from the SCOP and PDB (Brookhaven protein data bank) databases, and which are similar to the HSSP database discussed earlier. One new database, PDB90D-B, has domains that are <90% identical and the other, PDB40D-B, has domains that are <40% identical. Using various sequence alignment methods, each entry in each database was then used to search the rest of that database to discover how sensitive the method was at finding related sequences versus how many errors were made in misidentifying unrelated sequences. The alignment programs included SSEARCH (Smith-Waterman algorithm), BLAST, WU-BLAST, and FASTA and the standard or default scoring matrices and gap penalties of these programs. WU-BLAST2, a newer version of BLAST, uses gapped alignments (see Agarwal and States 1998 and Chapter 7 in the book).
The authors found that use of statistical scores provided a much improved ability to identify structural homology over raw alignment scores or percent identity. The statistical scores of SSEARCH and FASTA reliably predicted the actual number of incorrectly identified proteins. However, the statistical scores estimated by BLAST programs overestimated the significance by one or two orders of magnitude because many more unrelated proteins were found. The very best of the programs, SSEARCH and FASTA (k-tuple 1), using statistical scores could at best find only 18% of all related proteins in the PDB40D-B database at a 1% error rate. BLAST identifies 15% of the relatives, and the other programs were intermediate. In the PDB40D-B database, most of the structural homologs cannot be detected by sequence similarity because they have so little sequence similarity. SSEARCH detected hardly any structural homologs that have <15% identity, but could detect most that have >25% identity. Between 15 and 20% identity, 10% were identified, and between 20 and 25%, 40%. Thus, there is a limit to which sequence similarity searching can detect structural homologs that share little sequence similarity. For the PDB90D-B database, WU-BLAST identifed 38% at the 1% error level, with the older version of BLAST giving 28% and the other programs intermediate values.
The result with WU-BLAST is not surprising, because several scoring regions are likely to be found between the similar sequences in the PDB90D-B database. WU-BLAST uses this information to weight such information more significantly than older versions of BLAST. An interesting example of two proteins that have 39% identity over an alignment length of 64 residues, but which have different structures, is shown. The alignment scores given for this alignment were not significant. In general, because the databases are now so large, a level of 40% identity for alignments at least 70 residues in length is a reasonable threshold for structural similarity. The databases are available from http://scop.mrc-lmb.cam.ac.uk/scop/.
Pearson (1995) has performed the most detailed analysis to date of the ability of combinations of scoring matrices and gap penalties to assist in the recognition of proteins that are known to be in the same superfamily. Superfamily classification of proteins is performed by the PIR resource and is based on sequence similarity but also on other criteria, such as a similar structure, that provide an indication of an evolutionary relationship. Some members of the same superfamily share significant sequence similarity, but others may not. In such cases, two nonsimilar sequences may be found to have similarity with a third, in-between member of the same family, thus establishing a relationship among the three proteins. Due to such variations in similarity among related proteins, finding members of a family in a database search poses a difficult challenge. Pearson (1995) performed an extensive analysis of 67 superfamilies from the PIR1 database.
Pearson used the computer programs SSEARCH, FASTA, and BLAST, which are designed to be used in a database search and to identify proteins that are related to an input sequence. SSEARCH is an implementation of the Smith-Waterman algorithm, which searches an entire database for sequences that give the highest alignment scores. FASTA and BLAST perform the same function more rapidly by identifiying sequences that have short matching patterns or words in sequences, and then aligning them. These programs utilize various scoring matrices and gap penalty combinations and are discussed in greater detail in Chapter 7 in the book. The object of these studies was to compare the numbers of superfamily members found by the above programs in a database search, given as input of the sequence of a known family or superfamily member. Several different scoring matrices were tested, each with a set of gap penalties in the range -6, -1 to -16, -1, where -6 to -16 is the penalty for a gap of size 1 and there is an additional -1 for each additional gap position. The number of members found is a measure of the sensitivity of the program, scoring matrix, and gap penalty combination. A better combination of program and scoring system will also not find members of other superfamilies in a database search. This capability is a measure of the selectivity of the program and scoring system. A combined measure of sensitivity and selectivity called the equivalence number was used to compare the methods. This measure is the number of related sequences missed at a similarity score X which balances the number of low-scoring family sequences missed with the number of unrelated sequences with scores at or above X. The equivalence number was scored for each of the 67 families and the results were compared by a simple statistical test. Later, this measure was replaced by more informative and detailed statistical estimates of alignment scores (Pearson 1996, 1998).
In performing this analysis, Pearson (1995) also found that rescaling the alignment scores to adjust for an apparent increase in score with sequence length increased the sensitivity and selectivity of the search. These scaling methods were later improved when it became possible to perform a reliable statistical assessment of the alignment score (Pearson 1996, 1998).
The best combination of program and scoring system was the SSEARCH program (Smith-Waterman program optimized as described previously) in combination with the BLOSUM55 scoring matrix (which is in units of 1/3 bits like the PAM, Gonnet92, and JTT matrices), and gap penalties of -12, -2. The PAM250 matrix performed significantly worse at every gap penalty tested. In contrast, the JO93 (-10, -4 to -16,-2) and JTT160/JTT200 (-14, -2) combinations performed as well as BLOSUM55 (-12, -2). The higher PAM JTT matrices (JTT250 and 320) did not perform as well as BLOSUM55 (-12, -2). BLOSUM62 (-6,-4 and -8, -2) which is scaled in 1/2-bit units and thus requires smaller gap penalties, was almost, but not quite, as good as BLOSUM55 (-12, -2). When length-scaled scores were used, the BLOSUM45 (-10, -2; -12, -1; -12, -2) or Gonnet92 (same penalties) performed the best, and JO93 and JTT250 performed poorly. PAM250 (-10, -2; -12, -2; -14, -2) did not perform significantly worse than BLOSUM45 (-10, -2; -12, -1; -12, -2). Other scoring schemes, such as adding a small, positive value to the scoring matrix, or using a constant penalty for any size gap, or a constant penalty per gap position, did not perform as well as the above conditions. Pearson's results underscore the importance of using appropriate gap penalties. Besides having the undesirable effect of producing global instead of local alignments, low gap penalty, e.g., -8, -1 in the above study, decreased the selectivity of the method used and led to the erroneous estimates of statistical significance (Pearson 1998). Pearson later performed a detailed statistical analysis of alignment scores found in a database search by SSEARCH, using methods described in Chapter 7. BLOSUM50 (-12,-2) and BLOSUM50 (-14,-2) with rescaled similarity scores were the best combinations, the choice between these two depending on the method used to rescale the scores (Pearson 1998).
7. Use of scoring matrices for producing structural alignments
There have been several analyses of the effectiveness of scoring matrices to produce alignments that match alignments based on three-dimensional structures. Henikoff and Henikoff (1992) tested the ability of several PAM matrices and the BLOSUM62 matrix to generate a multiple sequence alignment that matched alignments known from the tertiary protein structure of serine proteases, and found that the BLOSUM62 misaligned fewer amino acids than the PAM 120, 160, or 250 matrices. Johnson and Overington (1993) prepared a scoring matrix (JO93) based on the alignments in 65 homologous sets of structurally aligned proteins that were 15% to 40% identical. They then compared the ability of this matrix with 12 other published matrices to predict the alignments observed among six sequences from each of three protein families. Both predicted pair-wise and multiple Needleman-Wunsch sequence alignments were analyzed for accuracy. The results were averaged from a series ofgap penalties chosen to provide the most significant alignments by a statistical test. However, only a single penalty was considered for each gap, different from the commonly used linear scale for increasing gap penalty with gap length. Thus, the alignments were not obtained by the standard method. Of the matrices examined, JO93 performed the best, but Gonnet92 and BLOSUM62 performed almost as well. Another structure-based matrix formulated by Risler (Risler et al. 1988) and the Fitch minimum base change matrix (Fitch 1966) performed the worst. Another interesting finding in these studies was that the accuracy of the matrices increased significantly if they were used to produce a multiple sequence alignment for a group, rather than separate pair-wise alignments.
Vogt et al. (1995) performed a similar study of scoring matrix accuracy using a set of 204 protein sequences that are 9-62% identical and in 37 protein families whose alignments were already reliably identified based on structural information. Of the 30 matrices tested, some were log odds matrices and others were matrices based on simple scoring schemes, such as chemical properties of amino acids. The authors first performed an extensive analysis of the optimum values of the gap opening penalty n and the gap extension penalty r for a large number of amino acid substitution matrices. The GCG Needleman-Wunsch alignment program GAP and the Smith-Waterman program BESTFIT were used to produce trial alignments of a set of 204 protein sequences that are 9-62% identical and in 37 protein families. The authors found that the response of both of these programs changed dramatically if the scoring matrix included both positive and negative values, as in the log odds scoring matrices, or just positive values, as in the simpler scoring matrices (i.e., if the average score of the matrix values was a negative number, a small positive number, or a large positive number). For the Smith-Waterman program, this result is not surprising because, as discussed above, one of the requirements for obtaining a reliable local alignment by dynamic programming is that the scoring matrix should include negative values. For each of the matrices, the gap penalties were varied over a wide range to find the combination of n and r that gave the closest match to the known correct alignments using either the Needleman-Wunsch or Smith-Waterman programs. End gap penalties were not included in the analysis. The more positive scoring matrices all were, as a class, much better at predicting the known alignments than the negative ones. To put the various matrices on a common, average-scoring basis, a constant was added to all values in low-scoring matrices that made all scores positive. Similarly, a constant was subtracted from high-scoring matrices that gave the new matrix a representative low average score. Thus, the Dayhoff log odds matrix, at PAM250, whose values vary from -8 to 17, average -0.8, was converted by adding 8 to positive matrix PAM250_P, whose values vary from 0 to 25, average 7.2. The values of the gap penalties n and r were again optimized by a trial and error procedure for both the Needleman-Wunsch and Smith-Waterman programs. The results of this analysis shown in Table S3.2 revealed that the percentage of residues correctly aligned was achieved by using optimized gap opening and extension penalties specific for each matrix. An increase in the percentage identified (A) was achieved in all of the highest-scoring matrices by converting the matrices to a modified form with all positive scores (B).
Table S3.2. Gap opening and extension penalties optimized for original and modified amino acid substitution matrices (Vogt et al. 1995).
| A. ORIGINAL MATRICES |
|
Matrix
|
g
|
Smith-Waterman r1
|
Mean correct2
|
g
|
Needleman-Wunsch r1
|
Mean correct2
|
| Gonnet92 |
7.5
|
0.4
|
59.0
|
14.0
|
0.2
|
61.1
|
| BLOSUM50 |
8.0
|
1.1
|
57.4
|
9.5
|
1.2
|
59.9
|
| Benner74 |
8.5
|
0.8
|
59.0
|
9.5
|
0.8
|
60.7
|
| Johnson |
10.5
|
1.0
|
54.5
|
11.5
|
1.0
|
56.5
|
| BLOSUM62 |
8.0
|
0.5
|
56.5
|
7.5
|
0.9
|
58.5
|
| STR |
8.0
|
0.5
|
54.3
|
9.0
|
0.5
|
56.4
|
| PAM250 |
6.0
|
1.3
|
56.7
|
11.0
|
0.5
|
59.2
|
| PAM120 |
5.5
|
1.3
|
51.5
|
6.0
|
1.4
|
53.7
|
|
| B. MODIFIED MATRICES |
|
Matrix
|
g
|
r1
|
Mean correct2
|
Change3
|
| Gonnet92_p |
6.0
|
0.8
|
63.6
|
2.5
|
| BLOSUM50_p |
9.5
|
0.6
|
63.3
|
3.4
|
| Benner74_p |
7.0
|
0.8
|
63.1
|
4.1
|
| Johnson_p |
17.5
|
0.16
|
63.0
|
6.5
|
| BLOSUM62_p |
10.0
|
0.6
|
62.9
|
4.4
|
| STR |
12.5
|
0.12
|
62.9
|
6.5
|
|
1 The gap extension formula used is wx = g + r (x - 1), where x is the gap length. The values shown were optimized for each matrix to give the maximum percentage of residues identified.
2The mean correct is the percentage of residues identified by structural superposition that were correctly aligned, averaged over all sequences relative to the number identfied.
3Percentage increase obtained by using modified instead of original matrix. All of the modified matrices were obtained by adding a constant to the original matrix so as to make all scores >0. The Smith-Waterman and Needleman-Wunsch methods gave approximately the same results.
|
In this analysis, optimization of the gap penalties was essential for reliable performance of a given matrix. The top scoring matrices shown in Table S3.2, part B, gave very little difference in performance. The Gonnet_p matrix consistently gave a slightly higher accuracy for alignments between sequences at different levels of similarity, i.e., at increasing levels of evolutionary divergence. By optimizing the gap penalties of Dayhoff matrices at increasing PAM distances, it was possible to compare their ability to align proteins at these distances. For alignments between proteins that were 50-80% identical, matrices of distances from 30 to 250 PAMs performed equally as well for sequences in the 50-100% range of identity and almost as well for aligning sequences in the 25 to 30% range.
One of the most challenging aspects of sequence alignments is to align as correctly as possible sequences that have diverged sufficiently that any remaining similarity is difficult to identify. Doolittle (1989) refers to this low level of similarity as the "twilight zone" of sequence alignment, where one cannot be sure whether the sequences are really homologous or whether the alignment is just a chance one that has no biological significance. On the basis of the above analysis, for identity levels >26%, the probability of an incorrect relationship being found is <10%, but at 23-25% identity, this probability increases to 25%, and at 20-25% identity, the probability is 50%.
In summary, the Vogt et al. study provides information regarding the use of amino acid scoring matrices for discovering structural alignments in proteins: (1) The amino acid scoring matrices derived from a previous alignment of proteins based on structural or family-based alignments are more useful than those based on a well-defined evolutionary model, such as the Dayhoff matrices; (2) the average value of the matrices should be increased to a small positive score; (3) an optimal gap penalty for the matrix should be found; (4) the alignment should be done using the Needleman-Wunsch global alignment method because the modified scoring system will not lend itself to finding a local alignment by the Smith-Waterman method. Examples of suitable choices for scoring matrices and gap penalties are found in the above tables. This analysis provides one set of procedures for performing sequence alignments, but should not be the only one attempted. There are also other methods for finding structural alignments between proteins that are discussed in Chapter 9 in the book. Following these procedures will not provide information that is suitable for evolutionary analysis.
8. Methods for calculating the parameters of the extreme value distribution
Before calculating the statistical significance of a local alignment score, it is first necessary to calculate K and l of the extreme value distribution that apply to that score. These parameters are defined by aligning many sequences that are not related using the same scoring system (scoring matrix or match and mismatch scores, and gap penalties) and an alignment program that uses the Smith-Waterman local alignment algorithm. These scores of unrelated sequences will then be plotted on a distribution plot that should have the appearance of the extreme value distribution, as depicted in Figure 3.22 in the book. Several types of unrelated sequences may be used. The second of the sequences may be randomly shuffled, maintaining the same amino acid or nucleotide composition and local sequence features, and the many shuffled sequences then realigned with the first. Because few if any of these shuffled sequences will be related to the first sequence, they provide the necessary range of scores for unrelated sequences. Alternatively, many random sequences may be generated and aligned with each other. Sometimes, random sequences of different lengths are generated to test an important theoretical feature of alignment scores, and the scores increase as the logarithm of the sequence length. Another method is to measure the distribution of the alignment scores of a set of random sequences of a given length. The total number with a score less than or equal to a score value x should decrease exponentially as x increases. These types of analyses will also reveal whether or not the scoring system in use is providing a local, as opposed to a global, alignment, because they will not work if global alignment scores are produced. Finally, a given sequence may be aligned in turn with every sequence in a sequence database library. If the related sequences are filtered out, the remaining unrelated sequences in the database can be used to calculate the statistical parameters. This is the method used by the SSEARCH program (which performs a full Smith-Waterman local alignment with every database sequence) and FASTA, vers. 3 program (Pearson 1996, 1998). The significance of an alignment score may be further analyzed by aligning a sequence with a shuffled library or a shuffled sequence with an unshuffled library. In contrast, note that the BLAST database searching program calculates the values of these parameters from theory using information from the scoring matrix, and the amino acid or nucleotide composition of the sequences used to prepare the scoring matrix. There are several ways to analyze the alignment scores from random and unrelated sequences to derive the parameters of the extreme value distribution.
One method, the method of moments, resembles that used to fit data to a normal curve by calculating the mean and standard deviation of the individual scores from the mean, which in statistical terms are known as the first and second moments of the normal distribution. The corresponding moments of the extreme value distribution are the center value u and the scaling parameter l The relationships between these moments are u = x - 0.4500σ and l = 1.2825σ (see Altschul and Erickson 1986). Therefore, one can calculate the mean and standard deviation of a set of alignment scores among random sequences in the usual way for a normal distribution, and then use these values to estimate u and l of the equivalent extreme value distribution.
Two other methods of evaluating the statistical parameters use the expectation that scores between random sequences will increase as the logarithm of the sequence length. One way is to align pairs of random sequences from a pool of sequences of approximately the same length, and then to use these scores to indicate the range of alignment scores for that length. Another is to align the first or second sequence of interest with a sequence library, noting the length of each library sequence. The lengths of both the test sequence and the length of the library sequence will influence the range of alignment scores. However, because the length of the test sequence is the same in each comparison, only the length of the library sequence will influence the range of scores found. As with random sequences, scores from alignments with library sequences of approximately the same length provide the range of scores for that length. The only additional requirement is that high scores from alignments of sequences related to the test sequence and of low-complexity sequences must be pruned from the distribution of scores. The mean score and standard deviation for each length range provide an estimate of the u and l, as described above. A better estimate is obtained by plotting the calculated values of u against the logarithm of the sequence length (log n) over the range of lengths found. This procedure should give a straight line
| u = (ln K)/l + ln (nm)/l |
(S5) |
Both l and K may be calculated by linear regression because the slope of the straight line is 1/l and the y intercept is (ln K)/l. A variation of this method is used in the SSEARCH and FASTA vers. 3 programs. Instead of calculating u and (ln K)/l for each length, the average score over a short range of sequence lengths is plotted against the logarithm of the average length in each range, log n. The resulting points are then fitted to a straight line by linear regression. Each score is then normalized by subtracting the predicted values along the fitted line from the alignment scores, and the variance of these scores from the fitted line is determined. Finally, each score is converted to z scores, where the z score is the number of standard deviations of an alignment score from the fitted line. At this point in the current implementation of this method (Pearson 1998), there are repeated prunings of high scoring, presumably related or less complex sequences, and also of very low scoring alignments that do not fit the straight line, and a recalculation of the z scores with these ones excluded.
A second method for estimating K and l is to use maximum-likelihood estimation (Mott 1992). In this case, trial but reasonable values for the parameters are used in the equation describing the extreme value equation to predict the distribution found in the data. Based on the goodness of fit, new trial values adjusted appropriately to provide a better fit to the data are then used. This procedure is repeated until parameters providing a good fit are found and the fit to the data cannot be further improved. Pruning of unusual low and high scores is also performed in this analysis. The programs are available from the author.
A novel, rapid method for estimating K and l is the Poisson approximation method. Scores from a series of best-scoring alignments between the same two random sequences are used (Waterman and Vingron 1994a, b). The idea is to align a few pairs of random sequences (say 10), but to find a large number of possible alignments from each pair (say 300). This procedure is much faster than aligning 3000 different pairs of random sequences, because once the dynamic programming scoring matrix has been established, all of the possible alignments are there. If the positions of the dynamic programming scoring matrix that give the highest scoring alignment are neutralized as described earlier, then the second best alignment may be easily found, and this procedure may be repeated many times. If the sequences are long enough, i.e., 900-nucleotide sequences, this so-called declumping procedure can be repeated 300 times in a relatively short computer run. These subsequent alignments are also independent because they do not intersect (i.e., do not both align the same residues).
As discussed previously, each locally aligned region between two sequences is a cluster or "clump" of different possible alignments having about the same score and starting at the same scoring matrix position, as illustrated by the alignment regions in Figure S3.5. The highest-scoring alignment a is removed, and the next highest scoring "clump" is found. If this clump is b or c, then some of the same sequence included in alignment a is again used, but in a different alignment. If alignment c is the next-high- scoring clump, then only new sequence is used. In the Poisson approximation method, alignment a is removed by rescoring the region of the matrix containing the alignment, and other overlapping clumps such as b and c with a are removed from consideration by using a Poisson approximation for the number of scores that is greater than the expected, average score (Waterman and Vingron 1994a,b). Using such methods, independent alignments using different sequence from the same scoring matrix can be used for calculation of statistical parameters.
|
Figure S3.5. Clumps of alignments in the dynamic programming scoring matrix. Each clump is a group of alignments that match at least some of the same sequence residues, and each alignment originates at the same position in the scoring matrix at the upper left end of the clump. Clumps b and c include parts of the sequences in common with a, marked by solid bars at the top and left of the matrix, but these common regions are aligned with a different sequence than in a. The alignments in clump d do not share any sequence in common with a, b, or c. Alignment scores from clumps a and d thus provide independent alignment scores for use in estimates of statistical parameters. Overlapping ones are removed as described in the text.
|
|
After this procedure is repeated with other sets of random sequences (say 10 times), the average number of sequence alignments Nave that exceed a threshold score t is determined. This number represents the mean value of a Poisson distribution (Waterman and Vingron 1994a,b). Thus, the average number of scores above a threshold t will yield a value for s, and in turn values for K and l, according to the following equations,
| Nave (S > t) = Kmn e -lt |
|
|
log (Nave)
|
= log (Kmn e -lt)
|
|
| |
= log (Kmn) + log (e -lt)
|
|
| |
= log (Kmn) - lt
|
(S6) |
from which l and K may be obtained by linear regression.
Waterman and Vingron also perform many alignments of random sequences of the same lengths, and keep track of the fraction of the aligned sequences that have a score P (S < t). By the Poisson approximation, P (S < t) = exp (-Kmne-lx). A log(-log) transformation provides a linear equation from which l and K may be calculated by linear regression.
| log [ - log P (S < t) ] = log (Kmn) - l t |
(S7) |
In the above equations, the y intercept is log (Kmn) and the slope is l, and K can be calculated from the sequence lengths. These methods both provide reliable estimates of the statistical parameters (Waterman and Vingron 1994a,b).
Another method (Waterman and Vingron 1994a,b) for calculating the parameters of the extreme value distribution is the Poisson approximation, illustrated below. As the alignment score increases, the fraction of values with scores up to that point also increases, thus giving an estimate of P (x < S). This fraction can be transformed by loge (-loge) and plotted against the score, to fit the linear relationship given in the above equations, as shown in Figure S3.6. After a standard linear regression analysis, the y intercept and slope can be determined. The y intercept gives an estimate of K as log (Kmn) and the slope is -l. In the example shown, the y intercept was 6.6 and the slope was -0.16. K was calculated by dividing e6.6 by the sequence lengths to give K = 0.014, and the value of l is 0.16. The mode is given by (log (Kmn)) / l = 6.6 / 0.16 = 41. For comparison, one may calculate these values by the method of moments. The average and standard deviation of all of the scores must be calculated, taking into account the number of times each score is found in the distribution. The mean was 43 and the standard deviation 9.5, giving by the above equations, u = 39, l = 0.14, and K = 0.004. These differences are not surprising considering the small sample size of 100 alignments of random sequences.
|
Figure S3.6. Linear regression of log (-log) transformation of fraction of alignment scores up to and including score S against score. These are scores of the example given below of lamc1.pro, 237 amino acids with 100 random assortments of p22c2.pro, 216 amino acids. For example, there are 43/100 random scores up to and including a score of 41. The log (-log) of 41 is -0.170, which is plotted on the graph at a score of 41. The slope of the curve is -l or 0.16 and the y axis intercept (not shown on graph) is log (Kmn) or 0.663. Because the sequence lengths m and n are known, Kmn = 757.5 and K = 0.015.
|
|
9. Analysis of global alignment scores by extreme value distribution
In a study discussed in the text and above, Abagyan and Batalov (1997) examined the distribution of alignment scores between all members of the HSSP protein sequence database, which is based on proteins of known structure and additional structurally similar proteins. Using a scoring system of normalized scoring matrices and gap penalties with end gaps not weighted, they observed that the alignment score produced by the Needleman-Wunsch algorithm followed the extreme value distribution. This result is not particularly surprising, because the best or optimal score of any measurement can be expected to follow this distribution (Altschul et al. 1994). The gap penalty scores found to be useful for the BLOSUM50 matrix (-13 to open the gap and -1 for each additional position) are also in the useful range for obtaining local alignments by the Smith-Waterman algorithm (Altschul and Gish 1996). Other measurements made in this same study, including the percent of identical amino acids in the alignment and the sequence similarity measure (gap penalty = 0), were normally distributed. The extreme value distribution of the alignment scores in this case suggests that the alignments were local, even though a global alignment algorithm was being used.
REFERENCES
Abagyan R.A. and Batalov S. 1997. Do aligned sequences share the same fold? J. Mol. Biol. 273: 355-368.
Agarwal P. and States D.J. 1998. Comparative accuracy of methods for protein sequence similarity search. Bioinformatics 14: 40-47.
Altschul S.F. and Erickson B.W. 1986. A nonlinear measure of subalignment similarity and its significance levels. Bull. Math. Biol. 48: 617-632.
Altschul S.F. and Gish G. 1996. Local alignment statistics. Methods Enzymol. 266: 460-480.
Altschul S.F., Boguski M.S., Gish W., and Wootton J.C. 1994. Issues in searching molecular databases. Nat. Genet. 6: 119-129.
Benner S.A., Cohen M.A., and Gonnet G.H. 1993. Empirical and structural models for insertions and deletions in the divergent evolution of proteins. J. Mol. Biol. 229: 1065-1082.
---. 1994. Amino acid substitution during functionally constrained divergent evolutionof protein sequences. Protein Eng. 7: 1323-1332.
Brenner S.E., Chothia C., and Hubbard T. 1998. Assessing sequence comparison methods with reliable structurally identified distant evolutionary relationships. Proc. Natl. Acad. Sci. 95: 6073-6078.
Chao K.-M., Hardison R.C., and Miller W. 1994. Recent developments in linear-space alignment methods: A survey. J. Comput. Biol. 1: 271-291.
Dayhoff M.O., Barker W.C., and Hunt L.T. 1983. Establishing homologies in protein sequences. Methods Enzymol. 91: 524-545.
Doolittle R.F. 1989. Similar amino acid sequences revisited. Trends Biochem. Sci. 14: 244-245.
Feng D.F., Johnson M.S., and Doolittle R.F. 1985. Aligning amino acid sequences: Comparison of commonly used methods. J. Mol. Evol. 21: 112-125.
Fitch W.M. 1966. An improved method of testing for evolutionary homology. J. Mol. Biol. 16: 9-16.
Fitch W.M. and Smith T.F. 1983. Optimal sequences alignments. Proc. Natl. Acad. Sci. 80: 1382-1386.
Gonnet G.H., Cohen M.A., and Benner S.A. 1992. Exhaustive matching of the entire protein sequence database. Science 256: 1443-1445.
Gotoh O. 1982. An improved algorithm for matching biological sequences. J. Mol. Biol. 162: 705-708.
Henikoff S. and Henikoff J.G. 1992. Amino acid substitution matrices from protein blocks. Proc. Natl. Acad. Sci. 89: 10915-10919.
---. 1993. Performance evaluation of amino acid substitution matrices. Proteins Struct. Funct. Genet. 17: 49-61.
Hirschberg D. 1975. A linear space algorithm for computing longest common subsequences. Commun. Assoc. Comput. Mach. 18: 341-343.
Huang X. and Miller W. 1991. A time-efficient, linear-space local similarity algorithm. Adv. Appl. Math. 12: 337-357.
Johnson M.S. and Overington J.P. 1993. A structural basis for sequence comparisons: An evaluation of scoring methodologies. J. Mol. Biol. 233: 716-738.
Jones D.T., Taylor W.R., and Thornton J.M. 1992. The rapid generation of mutation data matrices from protein sequences. Comput. Appl. Biosci. 8: 275-182.
Mott R. 1992. Maximum-likelihood estimation of the statistical distribution of Smith-Waterman local sequence similarity scores. Bull. Math. Biol. 54: 59-75.
Murzin A.G., Brenner S.E., Hubbard T., and Chothia C. 1995. SCOP: A structural classification of proteins database for the investigation of sequences and structures. J. Mol. Biol. 247: 536-540.
Myers E.W. and Miller W. 1988. Optimal alignments in linear space. Comput. Appl. Biosci. 4: 11-17.
Pascarella S. and Argos P. 1992. Analysis of insertions/deletions in protein sequences. J. Mol. Biol. 224: 461-471.
Pearson W.R. 1990. Rapid and sensitive sequence comparison with FASTP and FASTA. Methods Enzymol. 183: 63-98.
---. 1995. Comparison of methods for searching protein sequence databases. Protein Sci. 4: 1150-1160.
---. 1996. Effective protein sequence comparison. Methods Enzymol. 266: 227-258.
---. 1998. Empirical statistical estimates for sequence similarity searches. J. Mol. Biol. 276: 71-84.
Pearson W.R. and Lipman D.J. 1988. Improved tools for biological sequence comparison. Proc. Natl. Acad. Sci. 85: 2444-2448.
Risler J.L., Delorme M.O., Delacroix H., and Henaut A. 1988. Amino acid substitutions in structurally related proteins: A pattern recognition approach. J. Mol. Biol. 204: 1019-1029.
Sander C. and Schneider R. 1991. Database of homology derived protein structures and the structural meaning of sequence alignment. Proteins 9: 56-68.
Saqi M.A. and Sternberg M.J. 1991. A simple method to generate non-trivial alternate alignments of protein sequences. J. Mol. Biol. 21 9: 727-732.
Smith T.F. and Waterman M.S. 1981a. Identification of common molecular subsequences. J. Mol. Biol. 147: 195-197.
---. 1981b. Comparison of biosequences. Adv. Appl. Math. 2: 482-489.
Vingron M. and Waterman M.S. 1994. Sequence alignment and penalty choice: Review of concepts, case studies and implications. J. Mol. Biol. 235: 1-12.
Vogt G., Etzold T., and Argos P. 1995. An assessment of amino acid exchange matrices: The twilight zone re-visited. J. Mol. Biol. 249: 816-831.
Waterman M.S. and Eggert M. 1987. A new algorithm for best subsequence alignments with applications to tRNA-tRNA comparisons. J. Mol. Biol. 197: 723-728.
Waterman M.S. and Vingron M. 1994a. Rapid and accurate estimates of statistical significance for sequence database searches. Proc. Natl. Acad. Sci. 91: 4625-4628.
---. 1994b. Sequence comparison significance and Poisson distribution. Stat. Sci. 9: 367-381.
Waterman M.S., Smith T.F., and Beyer W.A. 1976. Some biological sequence metrics. Adv. Math. 20: 367-387.
|